Laplace Transform Chart
Laplace Transform Chart - Web this section is the table of laplace transforms that we’ll be using in the material. Eatsinkt k (s−a)2 +k2 8. If \(g\) is integrable over the interval \([a,t]\) for every \(t>a\), then the improper integral of \(g\) over \([a,\infty)\) is defined as \[\label{eq:8.1.1} \int^\infty_a g(t)\,dt=\lim_{t\to\infty}\int^t_a g(t)\,dt.\] Web table of laplace transforms f(t) 1 l[f(t)] = f(s) f(t) 1 s (1) aeat bebt a b l[f(t)] = f(s) s (s a)(s b) (19) eatf(t) u(t a) f(t a)u(t a) (t) (t t0) tnf(t) f(s a) (2) teat eas s (4) (3) tneat e asf(s) 1 (5) eat sin kt e st0 (6) eat cos kt dnf(s) ( \displaystyle\frac {1} { {s}} {\left\lbrace\int g { {\left ( {t}\right)}}\ {\left. Coskt s s2 +k2 7. U(t−a) e−as s a≥0 11. 16t2u(t — a) created date Web 1 s { ∫ g ( t) d t } t = 0. We give as wide a variety of laplace transforms as possible including some that aren’t often given in tables of laplace transforms. Coskt s s2 +k2 7. Eatcoskt s−a (s−a)2 +k2 9. Sn+1 5 e−at 1 (s+a) 6 te−at 1 (s+a)2 7 1 (n−1)!t n−1e−at 1 (s+a)n 81−e−at a s(s+a) 9 e−at −e−bt b−a (s+a)(s+b) 10 be−bt −ae−at (b−a)s (s+a)(s+b) 11 sinat a s2+a2 12 cosat s s2+a2 13 e−at cosbt s+a (s+a)2+b2 14 e−at sinbt. Web s.boyd ee102 table of laplace. Web this section is the table of laplace transforms that we’ll be using in the material. Web unit 1 first order differential equations unit 2 second order linear equations unit 3 laplace transform math differential equations unit 3: Eatsinkt k (s−a)2 +k2 8. {d} {t}\right.}\right\rbrace}_ { { {t}= {0}}} s1. \displaystyle\frac {1} { {s}} {\left\lbrace\int g { {\left ( {t}\right)}}\. 4t 2 sin 4t) 14. Sinkt k s2 +k2 6. Web unit 1 first order differential equations unit 2 second order linear equations unit 3 laplace transform math differential equations unit 3: Y + 4y' + 5y = 50t, yo 30. Web 1 s { ∫ g ( t) d t } t = 0. Y + 4y' + 5y = 50t, yo 30. 1 √ t r π s 10. Web 1 s { ∫ g ( t) d t } t = 0. Eatsinkt k (s−a)2 +k2 8. ∇^2u(x,y,z) = 0, where u(x,y,z) is the scalar function and ∇^2 is the laplace operator. We give as wide a variety of laplace transforms as possible including some that aren’t often given in tables of laplace transforms. To define the laplace transform, we first recall the definition of an improper integral. 5 cosh 2t— 3 sinh t l13. Sn+1 5 e−at 1 (s+a) 6 te−at 1 (s+a)2 7 1 (n−1)!t n−1e−at 1 (s+a)n 81−e−at a. General f(t) f(s)= z 1 0 f(t)e¡st dt f+g f+g fif(fi2r) fif U(t−a) e−as s a≥0 11. Web table of laplace transforms f(t) l(f(t)) or f(s) 1. 4t 2 sin 4t) 14. Web unit 1 first order differential equations unit 2 second order linear equations unit 3 laplace transform math differential equations unit 3: If \(g\) is integrable over the interval \([a,t]\) for every \(t>a\), then the improper integral of \(g\) over \([a,\infty)\) is defined as \[\label{eq:8.1.1} \int^\infty_a g(t)\,dt=\lim_{t\to\infty}\int^t_a g(t)\,dt.\] \displaystyle\frac {1} { {s}} {\left\lbrace\int g { {\left ( {t}\right)}}\ {\left. 16t2u(t — a) created date Web 1 s { ∫ g ( t) d t } t = 0. Web definition of the. Web 1 s { ∫ g ( t) d t } t = 0. \displaystyle\frac {1} { {s}} {\left\lbrace\int g { {\left ( {t}\right)}}\ {\left. Coskt s s2 +k2 7. Web unit 1 first order differential equations unit 2 second order linear equations unit 3 laplace transform math differential equations unit 3: General f(t) f(s)= z 1 0 f(t)e¡st dt. 1 √ t r π s 10. If \(g\) is integrable over the interval \([a,t]\) for every \(t>a\), then the improper integral of \(g\) over \([a,\infty)\) is defined as \[\label{eq:8.1.1} \int^\infty_a g(t)\,dt=\lim_{t\to\infty}\int^t_a g(t)\,dt.\] To define the laplace transform, we first recall the definition of an improper integral. Sn+1 5 e−at 1 (s+a) 6 te−at 1 (s+a)2 7 1 (n−1)!t n−1e−at. 16t2u(t — a) created date In the following sections we see how to use the table of laplace transformations to solve problems. Laplace transform about this unit the laplace transform is a mathematical technique that changes a function of time into a function in the frequency domain. {d} {t}\right.}\right\rbrace}_ { { {t}= {0}}} s1. Table of laplace transforms number f(t). General f(t) f(s)= z 1 0 f(t)e¡st dt f+g f+g fif(fi2r) fif 16t2u(t — a) created date In the following sections we see how to use the table of laplace transformations to solve problems. Eatsinkt k (s−a)2 +k2 8. Sn+1 5 e−at 1 (s+a) 6 te−at 1 (s+a)2 7 1 (n−1)!t n−1e−at 1 (s+a)n 81−e−at a s(s+a) 9 e−at −e−bt b−a (s+a)(s+b) 10 be−bt −ae−at (b−a)s (s+a)(s+b) 11 sinat a s2+a2 12 cosat s s2+a2 13 e−at cosbt s+a (s+a)2+b2 14 e−at sinbt. 4t 2 sin 4t) 14. Web unit 1 first order differential equations unit 2 second order linear equations unit 3 laplace transform math differential equations unit 3: 1 √ t r π s 10. Web table of laplace transforms f(t) 1 l[f(t)] = f(s) f(t) 1 s (1) aeat bebt a b l[f(t)] = f(s) s (s a)(s b) (19) eatf(t) u(t a) f(t a)u(t a) (t) (t t0) tnf(t) f(s a) (2) teat eas s (4) (3) tneat e asf(s) 1 (5) eat sin kt e st0 (6) eat cos kt dnf(s) ( U(t−a) e−as s a≥0 11. Sinkt k s2 +k2 6. To define the laplace transform, we first recall the definition of an improper integral. ∇^2u(x,y,z) = 0, where u(x,y,z) is the scalar function and ∇^2 is the laplace operator. 5 cosh 2t— 3 sinh t l13. Coskt s s2 +k2 7. We give as wide a variety of laplace transforms as possible including some that aren’t often given in tables of laplace transforms.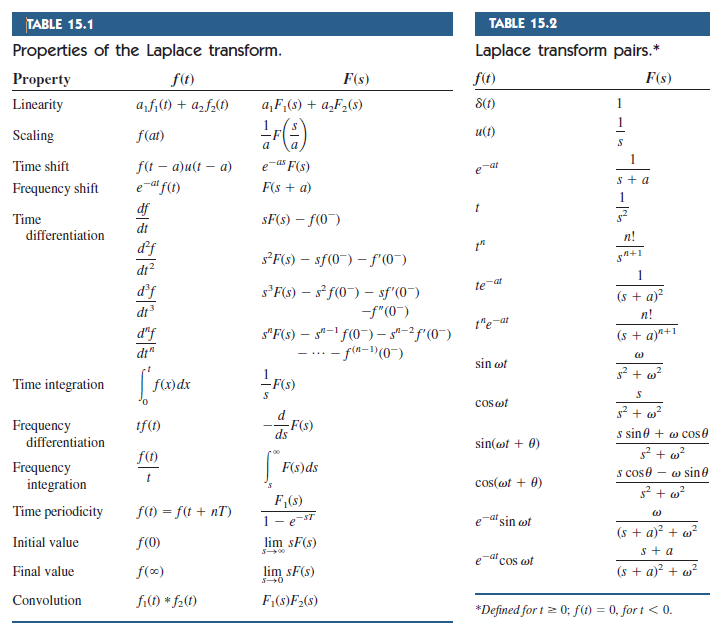
Laplace transform chart hipfreeloads
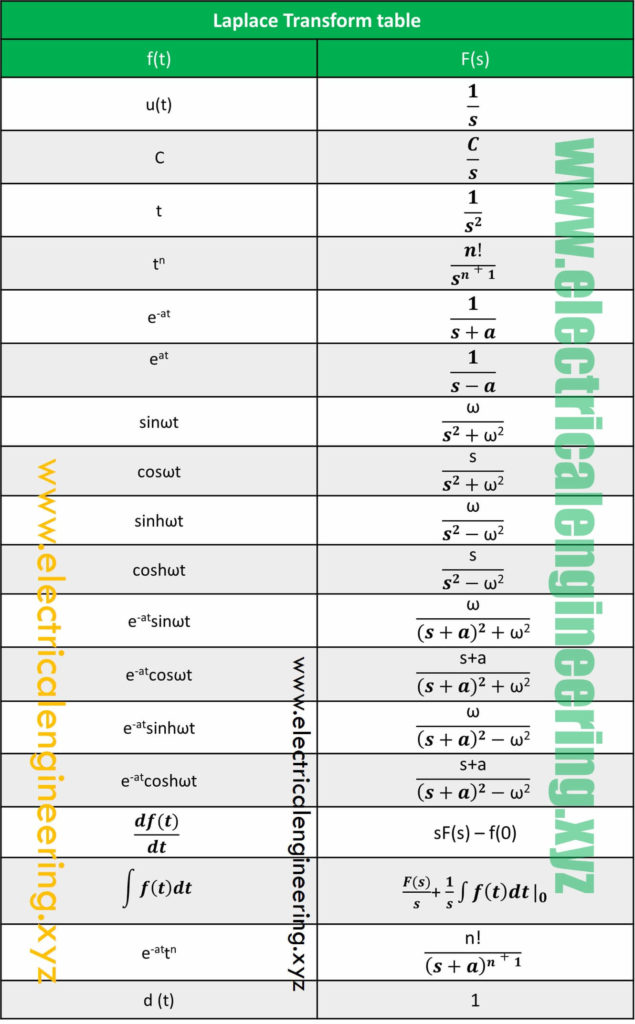
laplacetransformtableformulasheet • Electrical Engineering XYZ

Laplace table Laplace transform, Laplace, Physics and mathematics

Solving Differential Equations Using Laplace Transform Solutions dummies
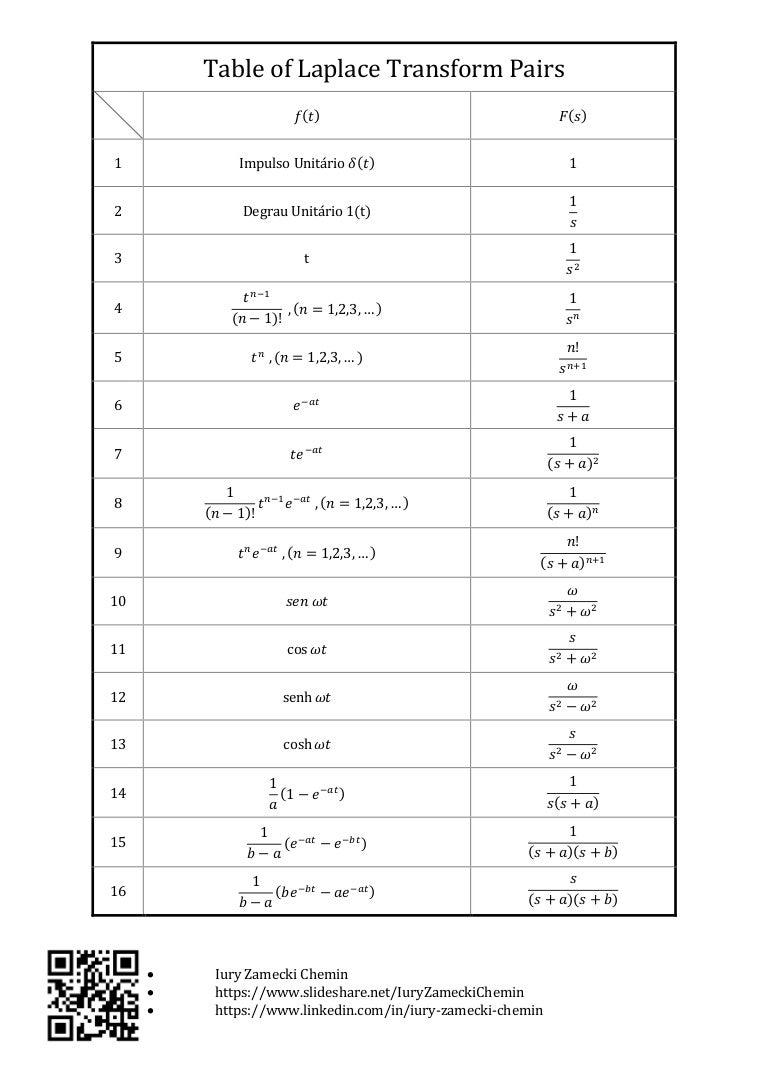
Table of Laplace Transform Pairs

Laplace Transform Full Formula Sheet

Solved 4 The Laplace transforms of some common functions.

Inverse Laplace Transform Table LandenrilMoon

Solved Determine the Laplace transform of the

Solved Use Laplace Transforms To Solve The Initial Value
Web S.boyd Ee102 Table Of Laplace Transforms Rememberthatweconsiderallfunctions(Signals)Asdeflnedonlyont‚0.
Table Of Laplace Transforms Number F(T) F(S) 1 Δ(T)1 2 Us(T) 1 S 3 T 1 S2 4 Tn N!
{D} {T}\Right.}\Right\Rbrace}_ { { {T}= {0}}} S1.
Laplace Transform About This Unit The Laplace Transform Is A Mathematical Technique That Changes A Function Of Time Into A Function In The Frequency Domain.
Related Post: