Quadric Surfaces Chart
Quadric Surfaces Chart - Now, let’s think about surfaces of the form \(r=c\). A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. You can also drag and rotate the axes to change your perspective. Find more mathematics widgets in wolfram|alpha. The ellipse, the parabola, and the. Surfaces that are the graphs of quadratic equations. When would i use this. Quadric surfaces in three dimensions are analogous to conic sections in two dimensions. Find more none widgets in wolfram|alpha. Y does not enter in the equation ! \nonumber \] when a quadric surface intersects a coordinate plane, the trace is a conic section. A quadric surface is an algebraic surface, defined by a quadratic ( order 2) polynomial. You can also drag and rotate the axes to change your perspective. Find more mathematics widgets in wolfram|alpha. When would i use this. Its most general form is: Web quadric surfaces are the graphs of equations that can be expressed in the form. Let’s look at the trace of the surface z = x2 on the plane y = k. All surfaces are symmetric with respect to the. Our collection contains most of the different types of quadric, including degenerate cases. You can also drag and rotate the axes to change your perspective. To sketch the graph of a quadric surface, start by sketching the traces to understand the framework of the surface. The ellipse, the parabola, and the. When a quadric surface intersects a coordinate plane, the trace is. They include important principle shapes such as those shown in figure. Ax2 + by2 + cz2 + dxy + eyz + fxz + gx + hy + iz + j = 0 for a through j constants. Get the free quadratic surfaces widget for your website, blog, wordpress, blogger, or igoogle. All surfaces are symmetric with respect to the. Web get the free quadric surfaces widget for your website, blog, wordpress,. You can also drag and rotate the axes to change your perspective. \nonumber \] when a quadric surface intersects a coordinate plane, the trace is a conic section. Its most general form is: Surfaces that are the graphs of quadratic equations. Quadric surfaces in three dimensions are analogous to conic sections in two dimensions. A quadric surface is an algebraic surface, defined by a quadratic ( order 2) polynomial. Examples of quadratic surfaces include the unit sphere x 2+ y2 + z = 1, the ellipsoid x 2+ y 2 9 + z 4 = 1 from above, and the cylinder x + y2 = 1, also. Let’s look at the trace of the. Every quadric surface can be expressed with an equation of the form a x 2 + b y 2 + c z 2 + d x y + e x z + f y z + g x + h y + j z + k = 0. A cylinder is a surface that consists of all lines that are. An example is the sphere \(x^2+y^2+z^2=1\text{.}\) here are some tables giving all of the quadric surfaces. Our collection contains most of the different types of quadric, including degenerate cases. Setting w = 1, this provides the ability to. Ax2 + by2 + c z2 + j = 0 or ax2 + by2 + i z = 0, where a, b,. Ax2 + by2 + cz2 + dxy + eyz + fxz + gx + hy + iz + j = 0 for a through j constants. You can also drag and rotate the axes to change your perspective. Move the sliders to change the coefficients of ax2 + by2 + cz2 = d a x 2 + b y 2. Quadric surfaces are the graphs of any equation that can be put into the general form \[a{x^2} + b{y^2} + c{z^2} + dxy + exz + fyz + gx + hy + iz + j = 0\] Ellipsoids theellipsoidis the surface given by equations of the form x2. They are the 3d counterparts of conic sections and have six distinct. Let’s look at the trace of the surface z = x2 on the plane y = k. Vectors and geometry in two and three dimensions. To sketch the graph of a quadric surface, start by sketching the traces to understand the framework of the surface. Ax2 +by2 +cz2 +dxy+exz+f yz+gx+hy+j z+k = 0 a x 2 + b y 2 + c z 2 + d x y + e x z + f y z + g x + h y + j z + k = 0. Web the three dimensional analogs of conic sections, surfaces in three dimensions given by quadratic equations, are called quadrics. The surface of equation z = x2. Find more mathematics widgets in wolfram|alpha. Find more none widgets in wolfram|alpha. A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. Every quadric surface can be expressed with an equation of the form a x 2 + b y 2 + c z 2 + d x y + e x z + f y z + g x + h y + j z + k = 0. When a quadric surface intersects a coordinate plane, the trace is. Y does not enter in the equation ! Setting w = 1, this provides the ability to. Now, let’s think about surfaces of the form \(r=c\). Web in this section we are going to be looking at quadric surfaces. Ax2 + by2 + c z2 + j = 0 or ax2 + by2 + i z = 0, where a, b, c, i, and j are constants.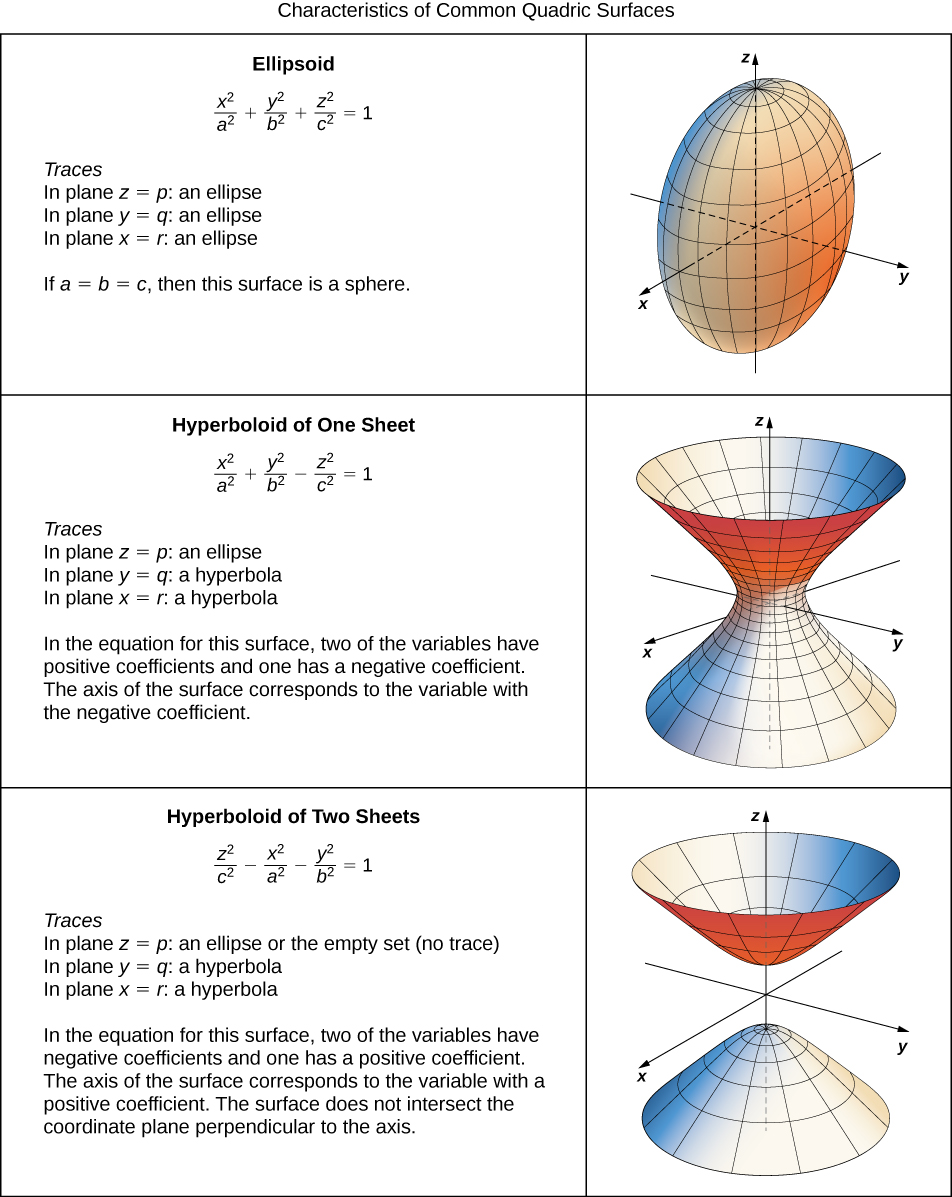
Ellipse Equation For Graphing Calculator Tessshebaylo

PPT Quadratic Surfaces PowerPoint Presentation, free download ID

Mary's Notes Learn physics, How to memorize things, Notes

Quadric surfaces YouTube

Quadric surfaces MATH 277

Vector Geometry Wize University Calculus 2 Textbook Wizeprep
![[PDF] TypeConstrained Direct Fitting of Quadric Surfaces Semantic](https://d3i71xaburhd42.cloudfront.net/44c43edcab0fca85ad5184866af596febea31b7b/3-Figure2-1.png)
[PDF] TypeConstrained Direct Fitting of Quadric Surfaces Semantic
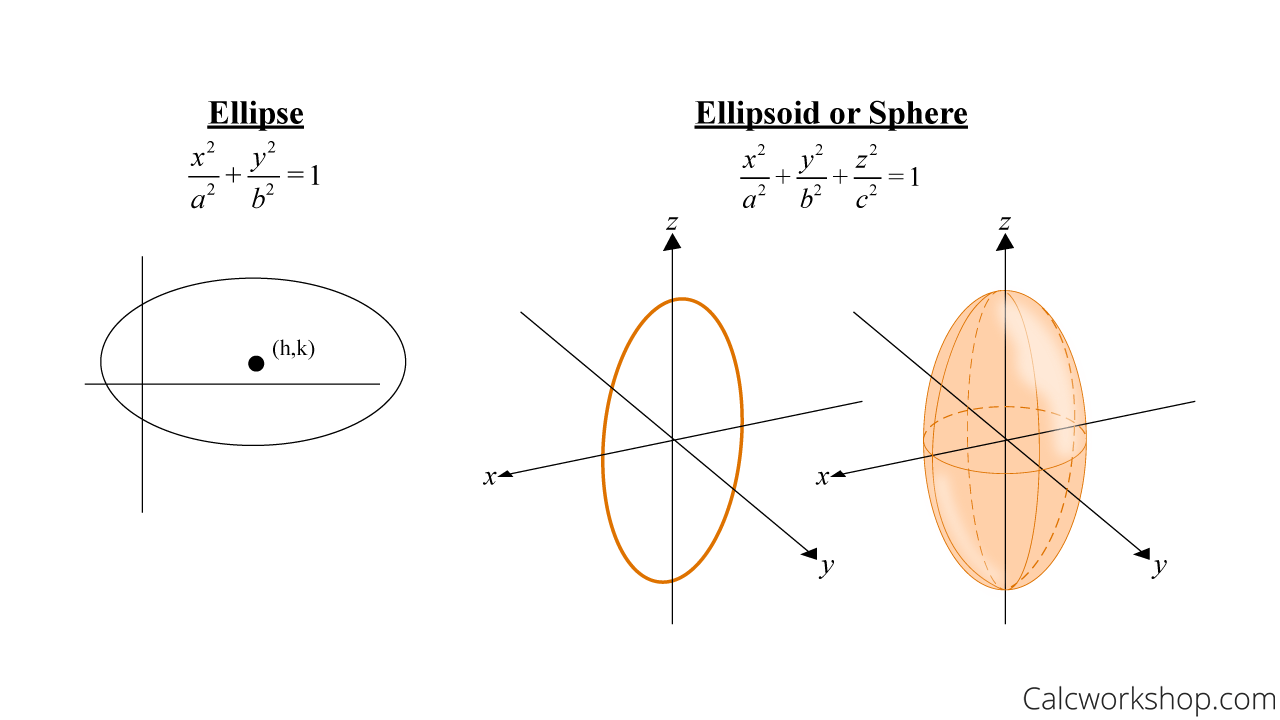
Quadric Surfaces (Identified and Explained w/ Examples!)
CIII E Graphs of Quadric Surfaces

Sketching graphs of quadric surfaces
Quadric Surfaces In Three Dimensions Are Analogous To Conic Sections In Two Dimensions.
All Surfaces Are Symmetric With Respect To The.
Web Quadric Surfaces Are The Graphs Of Equations That Can Be Expressed In The Form \[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Jz+K=0.
Its Most General Form Is:
Related Post:
